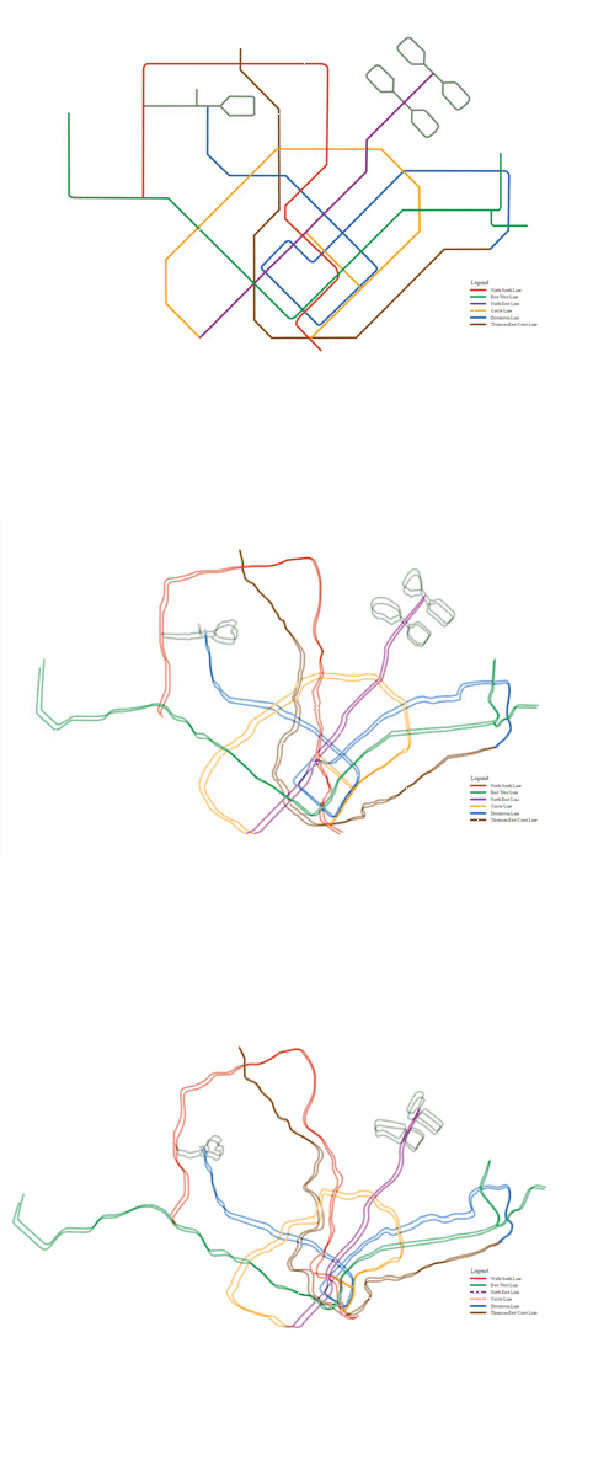
B06 | Adaptive Algorithms for Graph Views and View Transitions
Visualization of large graphs usually invokes simplification, aggregation, or pruning of substructures in order to reduce the visual complexity and to provide an informative overview to the user. This is especially true if additional data is visualized on top of or along with the graph, es e.g. flow values on the edges or node labels.
The best visualization of a graph crucially depends on the considered application. Often, a single graph view is not sufficient to provide the information content the user desires. So for comprehensive visual analytics, it is beneficial to provide different graph layouts for the user to choose from, as well as the possibility to specify
focus regions or to only visualize user-selected subgraphs.
But this level of flexibility poses a real challenge with respect to concistency between different graph views.
Our main goal is to develop new algorithms that allow user-customized graph views and smooth transitions between different types of graph visualizations.
Research Questions
How to optimize layouts for more visual consistency with respect to other layouts?
Given two graph views that result from optimizing a certain set of layout features each what is the best series
of intermediate graph views to morph the one view into the other?
What algorithms and data structures allow for real-time view transition (on demand)?
How much understanding can be gained by interactive graph view selection?
Fig. 1: From a schematized to a georgraphically accurate public transit network map: Intermediate views are helpful to identify correspondencies easier, especially in an animation.
Publications
- P. Paetzold, R. Kehlbeck, H. Strobelt, Y. Xue, S. Storandt, and O. Deussen, “RectEuler: Visualizing Intersecting Sets using Rectangles,” Computer Graphics Forum, vol. 42, Art. no. 3, 2023, doi: 10.1111/cgf.14814.
- Y. Zhang, K. Klein, O. Deussen, T. Gutschlag, and S. Storandt, “Robust Visualization of Trajectory Data,” it - Information Technology, vol. 64, pp. 181–191, 2022, doi: 10.1515/itit-2022-0036.
- P. Schäfer, N. Rodrigues, D. Weiskopf, and S. Storandt, “Group Diagrams for Simplified Representation of Scanpaths,” in Proceedings of the ACM Symposium on Visual Information Communication and Interaction (VINCI), ACM, Aug. 2022. doi: 10.1145/3554944.3554971.
- H. Bast, P. Brosi, and S. Storandt, “Metro Maps on Octilinear Grid Graphs,” in Computer Graphics Forum, Hoboken, New Jersey: Wiley-Blackwell - STM, 2020, pp. 357–367. doi: 10.1111/cgf13986.
- J. Spoerhase, S. Storandt, and J. Zink, “Simplification of Polyline Bundles,” in 17th Scandinavian Symposium and Workshops on Algorithm Theory, SWAT 2020, June 22-24, 2020, Tórshavn, Faroe Islands, 2020, pp. 35:1–35:20. doi: 10.4230/LIPIcs.SWAT.2020.35.
- M. Beck and S. Storandt, “Puzzling Grid Embeddings,” in Proceedings of the Symposium on Algorithm Engineering and Experiments, ALENEX 2020, Salt Lake City, UT, USA, January 5-6, 2020, 2020, pp. 94–105. doi: 10.1137/1.9781611976007.8.
- P. Angelini, S. Chaplick, S. Cornelsen, and G. Da Lozzo, “Planar L-Drawings of Bimodal Graphs,” in Graph Drawing and Network Visualization, D. Auber and P. Valtr, Eds., Cham: Springer International Publishing, 2020, pp. 205–219. doi: 10.1007/978-3-030-68766-3_17.
- S. Cornelsen et al., “Drawing Shortest Paths in Geodetic Graphs,” in Graph Drawing and Network Visualization, D. Auber and P. Valtr, Eds., Cham: Springer International Publishing, 2020, pp. 333–340. doi: 10.1007/978-3-030-68766-3_26.
- T. Stankov and S. Storandt, “Maximum Gap Minimization in Polylines,” in Web and Wireless Geographical Information Systems - 18th International Symposium, W2GIS 2020, Wuhan, China, November 13-14, 2020, Proceedings, 2020, pp. 181–196. doi: 10.1007/978-3-030-60952-8\_19.
- H. Bast, P. Brosi, and S. Storandt, “Efficient Generation of Geographically Accurate Transit Maps,” in Proceedings of the ACM International Conference on Advances in Geographic Information Systems (SIGSPATIAL), F. B. Kashani, E. G. Hoel, R. H. Güting, R. Tamassia, and L. Xiong, Eds., ACM, 2018, pp. 13–22. doi: 10.1145/3274895.3274955.
- D. Bahrdt et al., “Growing Balls in ℝd,” in Proceedings of the Meeting on Algorithm Engineering and Experiments (ALENEX), S. P. Fekete and V. Ramachandran, Eds., SIAM, 2017, pp. 247–258. doi: 10.1137/1.9781611974768.20.
- S. Funke, N. Schnelle, and S. Storandt, “URAN: A Unified Data Structure for Rendering and Navigation,” in Web and Wireless Geographical Information Systems. W2GIS 2017. Lecture Notes in Computer Science, vol. 10181, D. Brosset, C. Claramunt, X. Li, and T. Wang, Eds., 2017, pp. 66–82. doi: 10.1007/978-3-319-55998-8_5.
- S. Funke, T. Mendel, A. Miller, S. Storandt, and M. Wiebe, “Map Simplification with Topology Constraints: Exactly and in Practice,” in Proceedings of the Meeting on Algorithm Engineering and Experiments (ALENEX), S. P. Fekete and V. Ramachandran, Eds., SIAM, 2017, pp. 185–196. doi: 10.1137/1.9781611974768.15.
- S. Funke, A. Nusser, and S. Storandt, “On k-Path Covers and their Applications.,” VLDB Journal, vol. 25, Art. no. 1, 2016, doi: 10.1007/s00778-015-0392-3.
- S. Funke, F. Krumpe, and S. Storandt, “Crushing Disks Efficiently,” in Combinatorial Algorithms. IWOCA 2016. Lecture Notes in Computer Science, vol. 9843, V. Mäkinen, S. J. Puglisi, and L. Salmela, Eds., Springer International Publishing, 2016, pp. 43–54. doi: 10.1007/978-3-319-44543-4_4.
Project Group A
Models and Measures
Completed
Project Group B
Adaptive Algorithms
Completed
Project Group C
Interaction
Completed
Project Group D
Applications
Completed
FOR SCIENTISTS
Projects
People
Publications
Graduate School
Equal Opportunity
FOR PUPILS
PRESS AND MEDIA
SOCIAL MEDIA
© SFB-TRR 161 | Quantitative Methods for Visual Computing | 2019.