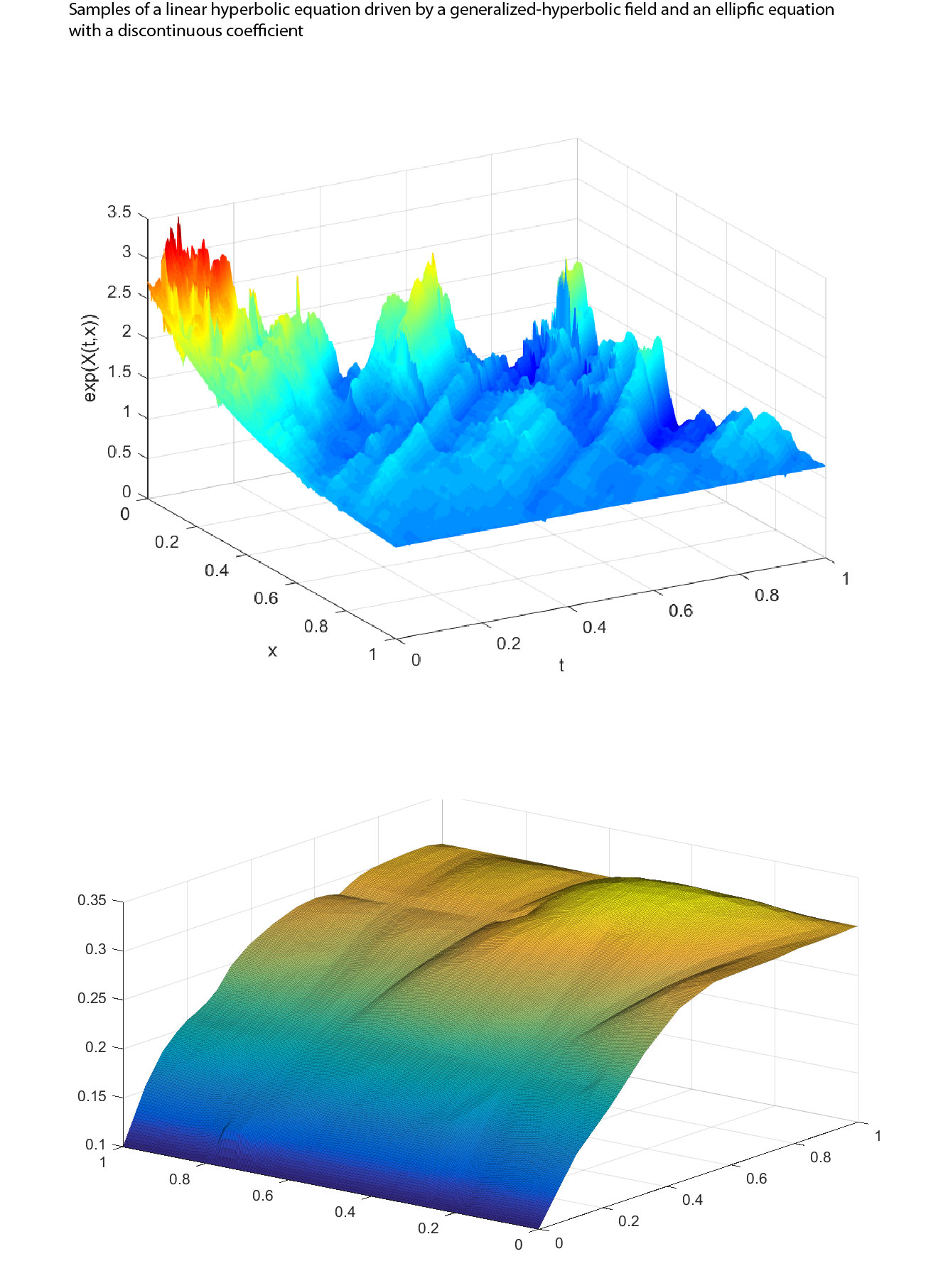
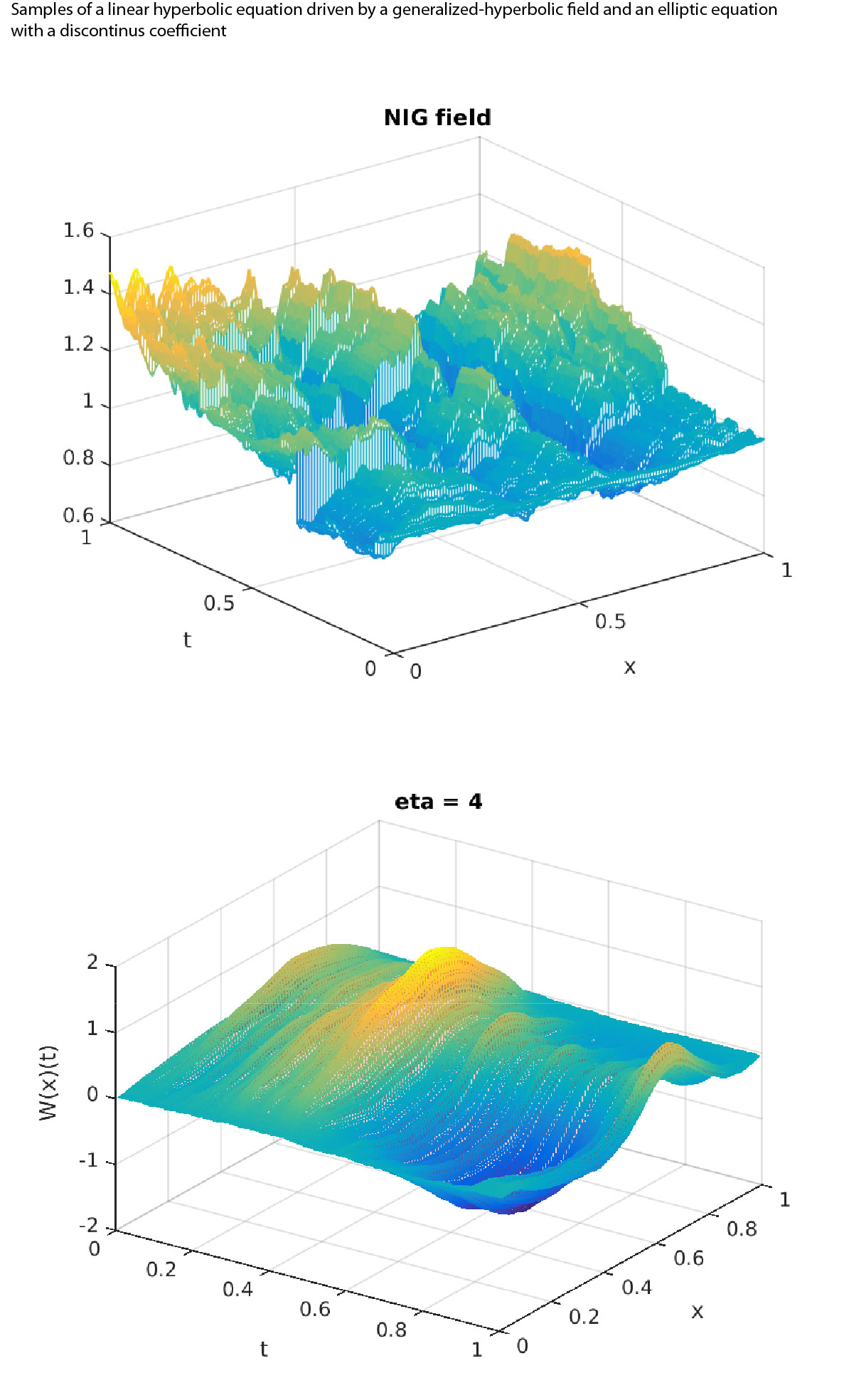
B07 | Computational Uncertainty Quantification
Every scientific visualization is based on data. The data may result from direct computation, numerical simulation, or be somehow measured.
The underlying model may be subject to various uncertainties, like parameter or domain uncertainty, model uncertainty, numerical errors, or some intrinsic stochasticity of the model. Further, the uncertainty is either introduced by the measurement instrument or is the result of insufficient measurements. In all cases, however, the data is just one representative sample of an underlying distribution, i.e., a repeated numerical simulation of a stochastic model may lead to a different sample of the same underlying distribution.
Uncertainty quantification is still lacking in interpretability and the discussion on appropriate problem-dependent risk measures in general.
As described above, visualizing uncertain problems is a problem of various aspects. The focus in this project lies on a rigorous mathematical modeling and a-priori error bounds for numerical simulations.
Project B07 aims to contribute to the following research topics:
- Sampling techniques for unknown distributions
- Non-linear transformations and risk measures:
- Inverse problems
The visualization of uncertain problems is investigated and further the influence of the visualization process on the said uncertainties.
Research Questions
How to sample efficiently for the visualization process?
How to approximate infinite-dimensional stochastic processes?
How is the visual computing pipeline influencing the uncertainties?
Fig. 1: Samples of a linear hyperbolic equation driven by a generalized-hyperbolic field and an elliptic equation with a discontinuos coefficient.
Fig. 2: Samples of a field with normal inverse Gaussian point-wise marginal distributions and Gaussian random field with different covariance operators.
Publications
- D. Hägele et al., “Uncertainty Visualization: Fundamentals and Recent Developments,” it - Information Technology, vol. 64, pp. 121–132, 2022, doi: 10.1515/itit-2022-0033.
- L. Mehl, C. Beschle, A. Barth, and A. Bruhn, “An Anisotropic Selection Scheme for Variational Optical Flow Methods with Order-Adaptive Regularisation,” in Proceedings of the International Conference on Scale Space and Variational Methods in Computer Vision (SSVM), in Proceedings of the International Conference on Scale Space and Variational Methods in Computer Vision (SSVM). Springer, 2021, pp. 140–152. [Online]. Available: https://link.springer.com/chapter/10.1007%2F978-3-030-75549-2_12
- A. Barth, B. Harrach, N. Hyvönen, and L. Mustonen, “Detecting Stochastic Inclusions in Electrical Impedance Tomography,” Inverse Problems, vol. 33, no. 11, Art. no. 11, 2017, doi: 10.1088/1361-6420/aa8f5c.
- A. Barth, R. Bürger, I. Kröker, and C. Rohde, “Computational Uncertainty Quantification for a Clarifier-thickener Model with Several Random Perturbations: A Hybrid Stochastic Galerkin Approach,” Computers & Chemical Engineering, vol. 89, pp. 11–26, 2016, doi: 10.1016/j.compchemeng.2016.02.016.
- A. Barth and A. Stein, “Approximation and simulation of infinite-dimensional Lévy processes,” Stochastics and Partial Differential Equations: Analysis and Computations, vol. 6, no. 2, Art. no. 2, 2016, doi: 10.1007/s40072-017-0109-2.
- A. Barth and F. G. Fuchs, “Uncertainty Quantification for Hyperbolic Conservation Laws with Flux Coefficients Given by Spatiotemporal Random Fields,” SIAM Journal on Scientific Computing, vol. 38, no. 4, Art. no. 4, 2016, doi: 10.1137/15M1027723.
Project Group A
Models and Measures
Completed
Project Group B
Adaptive Algorithms
Completed
Project Group C
Interaction
Completed
Project Group D
Applications
Completed
FOR SCIENTISTS
Projects
People
Publications
Graduate School
Equal Opportunity
FOR PUPILS
PRESS AND MEDIA
SOCIAL MEDIA
© SFB-TRR 161 | Quantitative Methods for Visual Computing | 2019.